Bits and Digital Circuits

---

Before diving into the world of quantum computing, it is helpful to first review some of the fundamentals of classical digital systems. This foundation will allow us to gradually introducing the key concepts that set quantum information systems apart from their classical counterpart.

Even if you have a solid understanding of Boolean logic and digital circuits, you might still find value in working through the first few chapters of this textbook will be valuable. Here, we not only revisit some basic concepts on classical computing but also explore how to incorporate uncertainty and probability into these systems and how logic gates can be modified to make operations reversible. These ideas are crucial for understanding quantum circuits and extend beyond a standard review of classical information processing.

1. Binary Numbers

All modern computers and communication systems rely on the use of binary numbers. The fundamental unit of a binary number is the bit, which can only take one of two values: \(0\) or \(1\). But just like with decimal numbers, we can express larger binary values by concatenating bits together. For example, with 3 bits, we can express up to 8 different binary numbers:

Binary	Decimal
\(000\)	\(0\)
\(001\)	\(1\)
\(010\)	\(2\)
\(011\)	\(3\)
\(100\)	\(4\)
\(101\)	\(5\)
\(110\)	\(6\)
\(111\)	\(7\)

In general, \(n\) bits allow us to express up to \(2^n\) different values. So, an \(n\)-bit binary number \(b\) can be represented as:

\[ b = b_{n-1} ... b_1 b_0 ,\]

where each bit \(b_i\) can take the value \(0\) or \(1\). We will often write this as \(b_i \in \{0, 1\}\).

In this definition of a binary number \(b\), the bit most to the right, \(b_0\), is known as the least significant bit (LSB). The bit most to the left, \(b_{n-1}\), is known as the most significant bit (MSB).

To convert a binary number \(b\) to a decimal integer \(x\), we simply take each individual bit, multiply it by \(2\) exponentiated to the bit’s significance, and then sum them all up:

\[ x = 2^{n-1} b_{n-1} + ... + 2^{1} b_{1} + 2^{0} b_{0}. \]

We can also write this expression more compactly as using big-sum notation:

\[ x = \sum_{i = 0}^{n-1} 2^{i} b_i .\]

For example, to represent the binary value \(b = b_3 b_2 b_1 b_0 = 1101\) in decimal, we write:

\[\begin{split} \begin{aligned} x &= 2^{3} b_{3} + 2^{2} b_{2} + 2^{1} b_{1} + 2^{0} b_{0} \\ \\ x &= 8 \times 1 + 4 \times 1 + 2 \times 0 + 1 \times 1 \\ \\ x &= 13 \end{aligned} \end{split}\]

Calculating this manually is a tedious process. Luckily we can use Python to perform these conversions for us. In Python we can represent binary numbers by using the prefix 0b. However, these values still get treated like any other integer. So, if we print them, we recover their corresponding decimal value. For example, we can save in a variable x the binary number 1101, and print it to see that it corresponds to 13:

x = 0b1101
print(x)

13

We can also take numbers in this binary representation and perform arithmetic operations like we do with decimal numbers. For example, we can add them together:

x = 0b1011 + 0b1001  # in decimal: 11 + 9 = 20
print(x)

20

Now, to convert a decimal integer \(x\) into a binary number \(b\), we can find the \(i^{\text{th}}\) bit of \(b\) using the following expression:

\[ b_i = \left\lfloor\frac{x}{2^i}\right\rfloor \text{mod } 2 . \]

If this equation looks intimidating, don’t worry, it really isn’t. Here, the symbol \(\lfloor \, \cdot \, \rfloor\) corresponds to the floor function, which returns the integer part of its input. For example \(\lfloor 2.71828 \rfloor = 2\). Furthermore, \(a \text{ mod } m\) represents the modulo operation, which returns the remainder of diving \(a\) by \(m\). For instance, \(5 \text{ mod } 2 = 1\) because \(5/2 = 2\) with a remainder of \(1\). The example below should clarify this further.

The full binary representation of \(x\) can then be found by multiplying each \(b_i\) by its corresponding power of \(10\), and adding them up:

\[ b = \sum_{i = 0}^{n-1} 10^{i} \left(\left\lfloor\frac{x}{2^i}\right\rfloor \text{mod } 2 \right).\]

As an example, to convert the decimal integer \(13\) into a 4-bit binary number, we would take:

\[\begin{split} \begin{aligned} b &= 10^{3} \left(\left\lfloor\frac{13}{2^3}\right\rfloor \text{mod } 2 \right) + 10^{2} \left(\left\lfloor\frac{13}{2^2}\right\rfloor \text{mod } 2 \right) + 10^{1} \left(\left\lfloor\frac{13}{2^1}\right\rfloor \text{mod } 2 \right) + 10^{0} \left(\left\lfloor\frac{13}{2^0}\right\rfloor \text{mod } 2 \right) \\ \\ b &= 10^{3} \left(1 \text{ mod } 2 \right) + 10^{2} \left(3 \text{ mod } 2 \right) + 10^{1} \left(6 \text{ mod } 2 \right) + 10^{0} \left(13 \text{ mod } 2 \right) \\ \\ b &= 1000 \times 1 + 100 \times 1 + 10 \times 0 + 1 \times 1 \\ \\ b &= 1101 \\ \end{aligned} \end{split}\]

One important note is that, in this example, we picked the exact number of bits (\(4\) bits) to get the correct binary representation for \(13\). However, if we would have picked \(n\) to be \(3\) or less, we would have ended up with the wrong binary representation for this number since there would not have been enough bits to fit it in. So, to guarantee we can correctly express a decimal integer (greater than \(0\)) in binary, we need to make sure to pick \(n\) to be:

\[ n \geq \lfloor \log_2 (x) + 1 \rfloor , \]

where, as we saw before, \(\lfloor \, \cdot \, \rfloor\) corresponds to the floor function. So, to accurately represent \(13\) in binary, we need \(n\) to be:

\[ n \geq \lfloor \log_2 (13) + 1 \rfloor = 4 . \]

Again, the concepts above are important to deepen our understanding, but we don’t need to go through the pain of calculating every one of these steps when we can simply rely on Python. So, to convert a decimal integer to binary, we can use the bin() function:

b = bin(13)
print(b)

0b1101

Now, one thing to note here is that the bin() function does not return an integer value, but rather a string of characters that represents our number in binary. For example, as we saw before, representing number \(13\) as 0b1101 returns an integer (in Python denoted as int):

print(type(0b1101))

<class 'int'>

whereas expressing \(13\) in binary using bin returns a string of characters (str):

print(type(bin(13)))

<class 'str'>

This means that we can’t really perform arithmetic operations directly on these objects and get the right result. For example, if we try to “add” two binary strings, Python treats the symbol + as a concatenation operator rather than numerical addition:

b = bin(11) + bin(9)  # in decimal: 11 + 9 = 20
print(f'The result in b: {b} is not the correct representation for the number 20: {bin(20)}')

The result in b: 0b10110b1001 is not the correct representation for the number 20: 0b10100

Therefore, we need to be careful when dealing with binary strings and always make sure they are in the right format when we want to perform certain operations. Now, luckily, we can always convert back a binary string into an integer in Python by using the int() function:

b = bin(13)  # converts 13 into a binary string
print(f'value in binary: {b}')
x = int(b, 2) # converts the binary string back to an integer
print(f'value in decimal: {x}')

value in binary: 0b1101
value in decimal: 13

Notice that when we did int(b, 2), we not only passed the value b which we want to convert back to decimal, but also base that number is expressed in (in this case, base 2 for binary). So, if we have binary strings and want to perform certain operations on them, we can always convert them back to decimal integers using this function, and then convert them back to binary strings.

It is also worth noting that the strings we pass to the int function do not necessarily have to have the prefix 0b. For instance:

b = '1101'
print(int(b,2))

13

This means that we can drop the 0b prefix of a binary representation without having to worry about including it again if we need to convert the value back to decimal. Since strings in Python are indexable, we can easily do this by simply storing the portion of string after the first two characters:

b = bin(13)[2:] # The square brakets [2:] index the string from the 2nd character on. 
print(b)

1101

Another important aspect of using the bin() function is that it always returns a string using the minimum number of bits required to represent the input number. For instance, notice how the number of bits changes below from 1 to 3 as we increase the decimal value:

for i in range(2**3):
    b = bin(i)[2:]
    print(f'{i}: {b}')

0: 0
1: 1
2: 10
3: 11
4: 100
5: 101
6: 110
7: 111

However, we will often want to express different binary numbers using a fix number of bits. For this, we can pad our string with zeros by using the zfill() method:

n = 4  # number of bits to use
for i in range(2**3):
    b = bin(i)[2:].zfill(n)
    print(f'{i}: {b}')

0: 0000
1: 0001
2: 0010
3: 0011
4: 0100
5: 0101
6: 0110
7: 0111

Alternatively, we can make use of the first library we will introduce in this textbook: NumPy. NumPy is a Python library optimized for numerical computation of multi-dimensional arrays and matrices. NumPy also counts with a large number of useful functions, including one to convert decimal numbers to binary strings of an arbitrary length.

Below, we first import NumPy using the alias np, and the make use of the function binary_repr() which takes as an input the decimal integer we want to convert, and the number of bits to represent it. For example, if we want the number \(13\) represented in \(5\) bits, we get \(01101\):

import numpy as np

b = np.binary_repr(13, 5)
print(b)

01101

Now that we have developed an understanding of how to use binary numbers in Python, we can discuss the types of operations we can perform on them and how are these implemented in the form of digital circuits.

2. Boolean Logic

Boolean logic is the type of algebra used to operate on binary numbers. In Boolean logic, variables can take one of two possible values: True or False, which are commonly represented with the values we previously assigned for the bit: \(1\) or \(0\), respectively.

There are three basic operations associated with Boolean algebra: Negation (NOT), Disjunction (OR), and Conjunction (AND).

The NOT operation is unary, meaning that it operates only on one variable by negating its value. There are many different symbols used to represent negation, but here we will denote it by using a bar over the variable being negated. A convenient way to express Boolean operations is by the use for Truth tables; the one below corresponds to that of the NOT operation:

\(a\)	\(\bar{a}\)
\(0\)	\(1\)
\(1\)	\(0\)

The OR operation is binary (operates on two variables), and results in a True statement when either of the variables are True (i.e., either of them is equal to \(1\)). Again, there are many different symbols to represent disjunction, but here we will use \((a \lor b)\) to denote \(a\) OR \(b\):

\(a\)	\(b\)	\(a \lor b\)
\(0\)	\(0\)	\(0\)
\(0\)	\(1\)	\(1\)
\(1\)	\(0\)	\(1\)
\(1\)	\(1\)	\(1\)

The AND operation is also binary, but only results in a True statement if both of the variables are True. We express this operation as \((a \land b)\):

\(a\)	\(b\)	\(a \land b\)
\(0\)	\(0\)	\(0\)
\(0\)	\(1\)	\(0\)
\(1\)	\(0\)	\(0\)
\(1\)	\(1\)	\(1\)

We can then combine these three basic operations to generate any possible logical statement between an arbitrary number of bits. For example, the 3-bit truth table below describes a statement that is True only when the majority of the bits are False.

\(a\)	\(b\)	\(c\)	\((\bar{a} \land \bar{b}) \lor (\bar{a} \land \bar{c}) \lor (\bar{b} \land \bar{c}) \)
\(0\)	\(0\)	\(0\)	\(1\)
\(0\)	\(0\)	\(1\)	\(1\)
\(0\)	\(1\)	\(0\)	\(1\)
\(0\)	\(1\)	\(1\)	\(0\)
\(1\)	\(0\)	\(0\)	\(1\)
\(1\)	\(0\)	\(1\)	\(0\)
\(1\)	\(1\)	\(0\)	\(0\)
\(1\)	\(1\)	\(1\)	\(0\)

It is worth pointing out that Boolean statements can always be simplified to use the least amount of literals as possible by using a combination of Boolean Algebra laws and De Morgan’s laws, but we will not go into these details herein.

A very important composite Boolean operation that we will use aplenty throughout the textbook is the Exclusive Disjunction, or Exclusive OR (XOR). The XOR operation is True if only one of the two variables is True.

\(a\)	\(b\)	\(a \oplus b\)
\(0\)	\(0\)	\(0\)
\(0\)	\(1\)	\(1\)
\(1\)	\(0\)	\(1\)
\(1\)	\(1\)	\(0\)

The XOR is a composite operation is because it can be expressed in terms of NOT, OR and AND operations as follows:

\[ a \oplus b = (a \land \bar{b}) \lor (\bar{a} \land b) .\]

However, when using binary values, the XOR operation is also equivalent to the addition operation modulo \(2\):

\[ a \oplus b = (a + b) \text{ mod } 2. \]

When dealing with binary numbers of more than one bit, we will assume Boolean logic operators act bitwise (i.e., on a bit-by-bit basis). So, for example, if we have two 3-bit numbers \(a = a_2 a_1 a_0\) and \(b = b_2 b_1 b_0\), the operation \(a \oplus b\) represents the bitwise XOR between the two:

\[\begin{split} \begin{aligned} c &= a \oplus b \\ c_2 c_1 c_0 &= (a_2 a_1 a_0) \oplus (b_2 b_1 b_0) , \end{aligned} \end{split}\]

where \(c_i = a_i \oplus b_i\).

The table below summarizes the bitwise operator symbols used in Python, followed by some examples:

Operator	Python
AND	&
OR	|
XOR	^

a = 0b11010
b = 0b10110

c_and = np.binary_repr(a & b, 5)  # Bitwise AND: 11010 & 10110 = 10010
c_or = np.binary_repr(a | b, 5)   # Bitwise OR:  11010 | 10110 = 11110
c_xor = np.binary_repr(a ^ b, 5)  # Bitwise XOR: 11010 ^ 10110 = 01100

print(f'a AND b = {c_and}') 
print(f'a OR  b = {c_or}')
print(f'a XOR b = {c_xor}')

a AND b = 10010
a OR  b = 11110
a XOR b = 01100

NOTE: Something very important to highlight is that, the Python logical operators and and or are not equivalent to the bitwise operators & and ^ when applied to binary integers of more than one bit. Understanding how these operators act on binary integers is irrelevant to the current discussion, but if you’re curious about it, you can check this Stack Overflow post.

3. Digital Circuits

Digital circuits are a diagrammatic representation of Boolean logic operations that can be directly translated into a physical implementation using electronic hardware. Understanding circuits is of great interest to us because different computational problems can be mapped onto this model, facilitating their classification into different complexity classes by using circuit complexity theory. As we will see in later chapters, this approach is widely used to analyze the type of advantage quantum algorithms can offer over a classical approach.

Classical circuits are constructed by interconnecting fundamental logic gates associated with the three basic Boolean operations: NOT, OR, AND. The figure below shows the gate symbols for these three operators (from left to right):

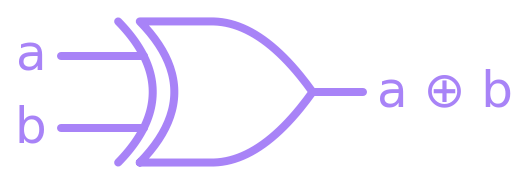
Similarly, the XOR operator is so widely used that it has its own symbol, even though it can be constructed out of NOT, OR and AND gates:

Another schematic simplification is to use a circle at the inputs or output of the binary gates to “absorb” a negation. For example, a AND / OR / XOR gate immediately followed by a NOT gate can be represented as:

These three gates are common enough that receive the names NAND / NOR / XNOR.

Using only these fundamental gates, we can then compose digital circuits for more complicated Boolean operations. For example, let’s say we want to construct a circuit that takes two bits \(a\), \(b\), and an input carry \(c_{in}\), and adds them into an output \(s\) and an output carry \(c_{out}\). We can express this in the form of a truth table:

\(a\)	\(b\)	\(c_{in}\)	\(s\)	\(c_{out}\)
\(0\)	\(0\)	\(0\)	\(0\)	\(0\)
\(0\)	\(0\)	\(1\)	\(1\)	\(0\)
\(0\)	\(1\)	\(0\)	\(1\)	\(0\)
\(0\)	\(1\)	\(1\)	\(0\)	\(1\)
\(1\)	\(0\)	\(0\)	\(1\)	\(0\)
\(1\)	\(0\)	\(1\)	\(0\)	\(1\)
\(1\)	\(1\)	\(0\)	\(0\)	\(1\)
\(1\)	\(1\)	\(1\)	\(1\)	\(1\)

It is not difficult to show that \(s = a \oplus b \oplus c_{in}\), which is expected since the XOR operation is equivalent to addition modulo \(2\). Finding the expression for \(c_{out}\) is slightly more involved since it requires synthesizing a Boolean expression by using methods like the sum of products conversion or Karnaugh maps, which we will not cover here. It suffices to say that it can be shown that \(c_{out} = ((a \oplus b) \land c_{in}) \lor (a \land b) \), which results in the circuit shown below:

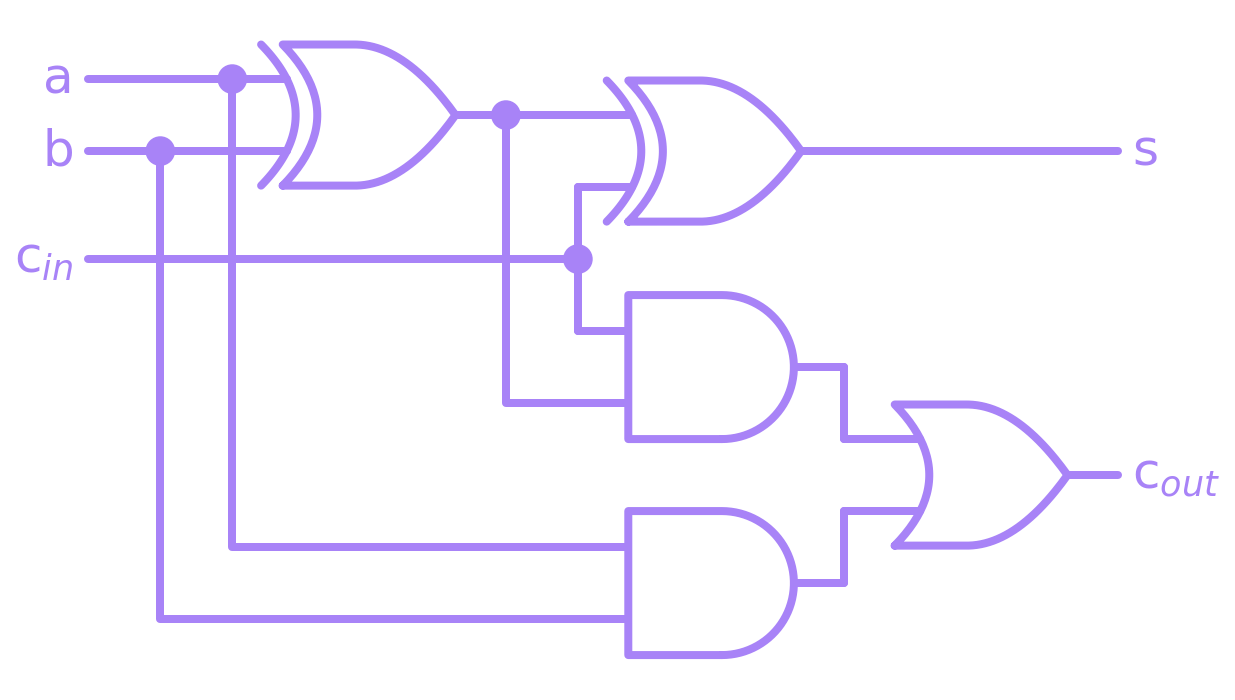
A concept that we have not yet discussed but is commonly utilized in circuit complexity analysis is that of the COPY or FAN-OUT operation. In the circuit above, we see that, for example, the variable \(a\) is used as an input on two separate gates. This variable was copied (or fanned-out) when a single wire turned into two separate ones:

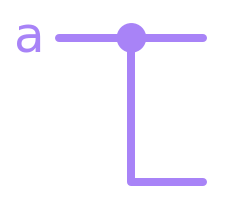
From a schematic standpoint, this might seem trivial considering that this will only require connecting an additional wire. However, from the point of complexity analysis this is an important operation because, as we will see later, there is no equivalent to the COPY operation in quantum circuits.

The key insight of being able to implement more complex Boolean circuits out of fundamental logic gates is that we can follow this process to construct all the building blocks of modern classical computing systems. Using only these gates, we can not only develop all the combinatorial logic used to build, for example, the core arithmetic logic unit (ALU) in a central processing unit (CPU), but also all sequential logic (latches, flip-flops, registers) required to store and parse its data.

4. Physical Implementation of Circuits

At a physical level, digital logic gates are not fundamental. Instead, they are implemented using transistors. The idea of this section is not to go into the details of how these devices work, but to provide some basic understanding on how they can be used to process Boolean information. This will later help us understand how quantum processors differ from classical devices at the hardware level.

Most modern integrated circuits are implemented using what is known as CMOS technology, where CMOS stands for complementary metal–oxide–semiconductor. CMOS circuits are implemented using two types of transistors: NMOS transistors, and PMOS transistors. For the current discussion, all we need to know is that transistors work like switches with two possible states: ON or OFF. NMOS and PMOS transistors are complementary devices, meaning that the level of voltage that turns one of these devices ON, turns the other one OFF, and vice versa. This is best exemplified by looking at the circuit used to construct a NOT gate:

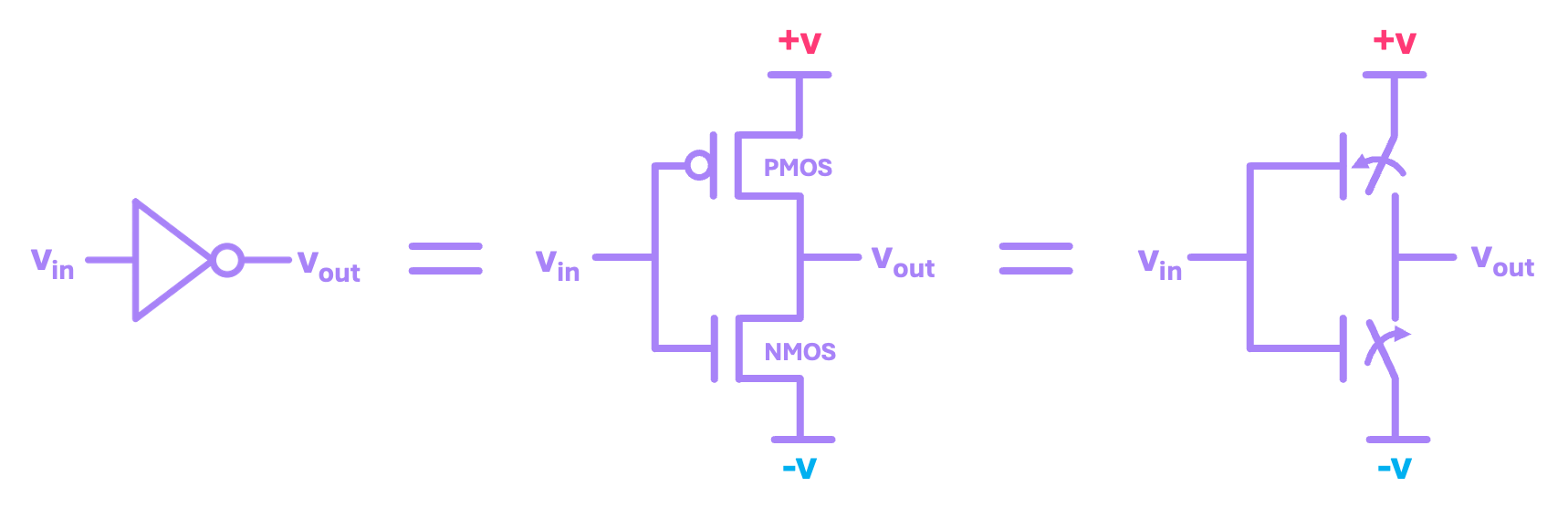
In this circuit, every node can take one of two possible voltages, \(+v\) and \(-v\), which we associate with a logical \(1\) and a logical \(0\), respectively. When the input voltage \(v_{in}\) is equal to \(+v\) (logical \(1\)), the NMOS transistor turns ON and the PMOS transistor turns OFF. This creates a direct connection between the negative power supply at \(-v\) (logical \(0\)) and the output, therefore effectively negating the logical value of the input:

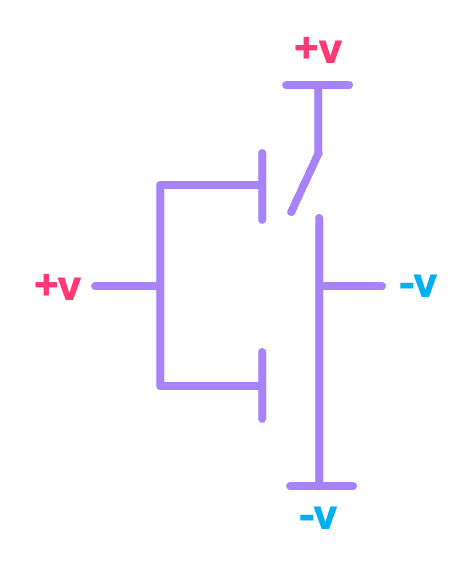
Similarly, when the input voltage \(v_{in}\) is equal to \(-v\) (logical \(0\)), the PMOS transistor turns ON and the NMOS transistor turns OFF, creating a direct connection between the positive power supply at \(+v\) (logical \(1\)) and the output, once again negating the logical value of the input:

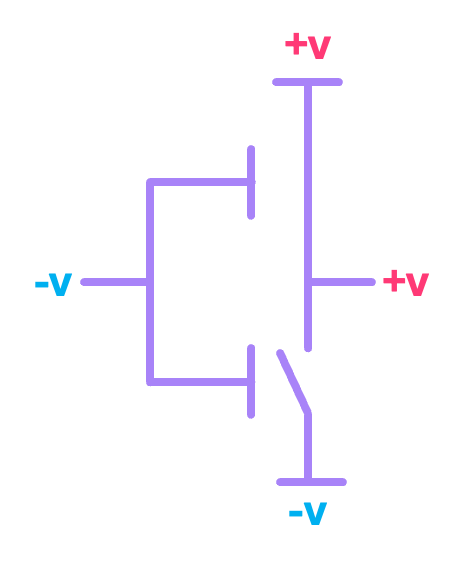
We can then use this same idea to construct other fundamental gates. For example, a NAND can be easily implemented using only 4 transistors:

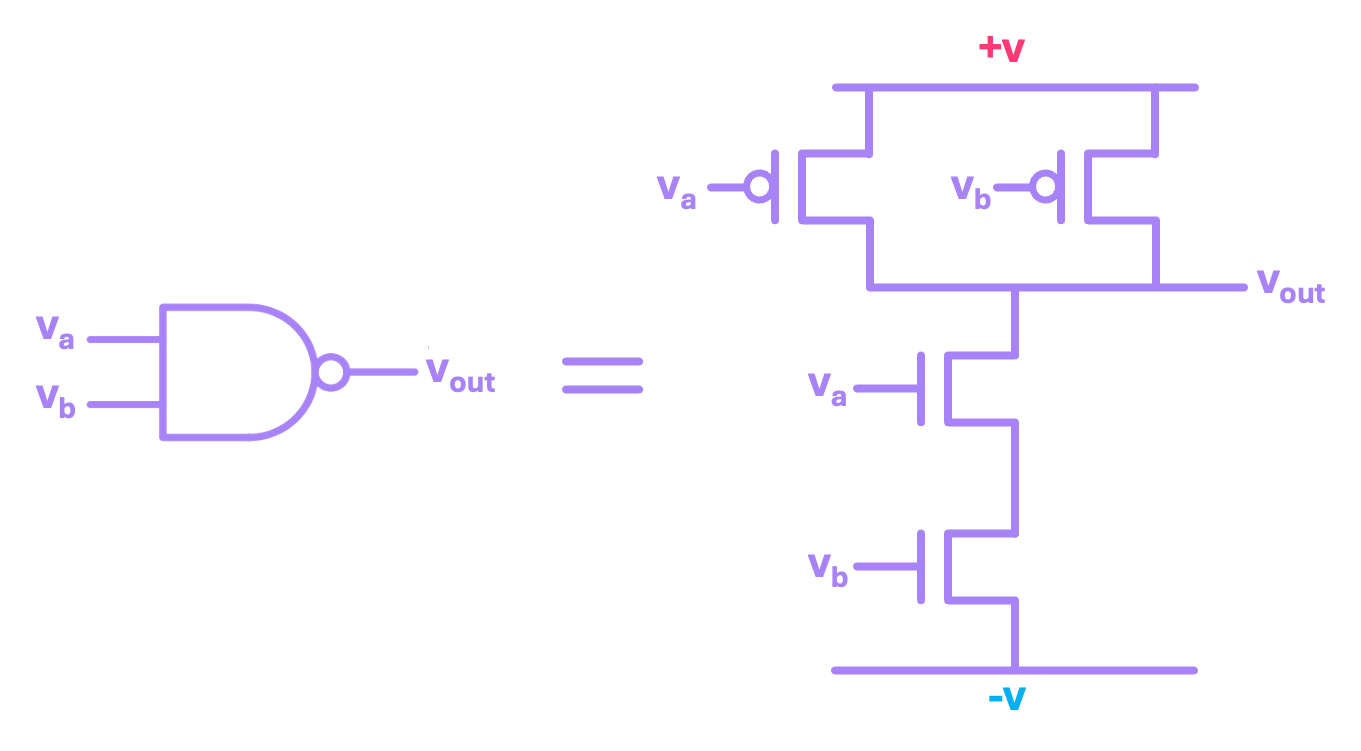
Same is true for a NOR circuit. A good exercise is to verify that the circuit above does in fact implement the NAND operation, and then try to implement the circuit for a NOR.

With these basic blocks, we can then interconnect them together to create any circuit we want. For example, we can implement an AND gate by connecting the input of a NOT circuit to the output of a NAND circuit:

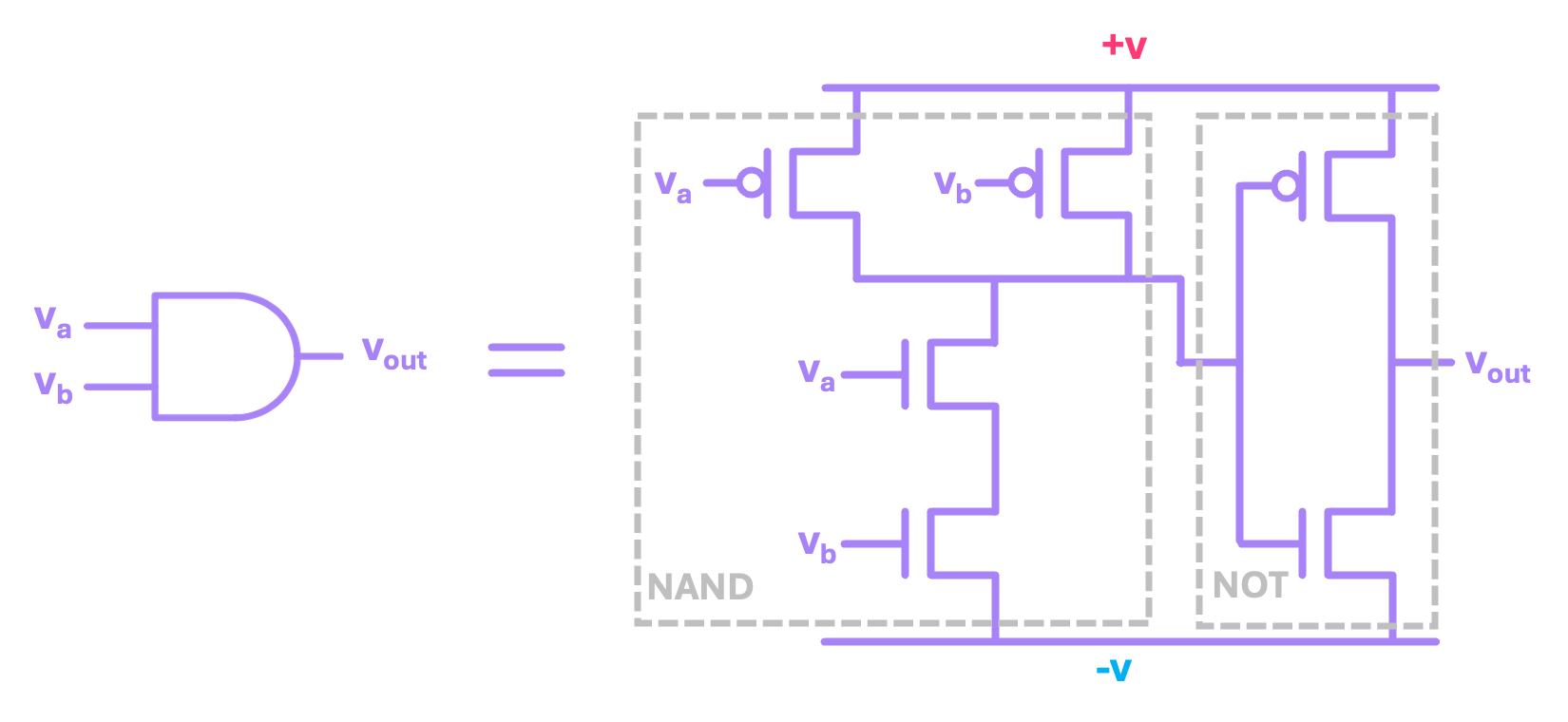
The main takeaway is that, at the hardware level, the binary values \(0\) and \(1\) are nothing other than two discrete voltage levels (here denoted as \(-v\) and \(+v\)). Transistors can then be arranged in circuits where input voltages turn them ON and OFF (like switches). This in turn modifies the voltage of an output node in a way that the input/output relation corresponds to a logic operation.

In the next chapter, we will continue to build our understanding towards quantum computing. An important step in this process is to introduce a different model of computation known as reversible computing. This is an important step in this process because the physical implementation of quantum hardware relies on quantum mechanics, which in principle is a reversible theory and therefore its model of computation should be reversible too.